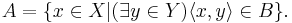Analytic set

This article is about analytic sets as defined in descriptive set theory. There is another notion in the context of analytic varieties.

In descriptive set theory, a subset of a Polish space $X$ is an analytic set if it is a continuous image of a Polish space. These sets were first defined by Luzin (1917) and his student Souslin (1917).

1 Definition
2 Properties
3 Projective hierarchy
4 References

Definition

There are several equivalent definitions of analytic set. The following conditions on a subspace A of a Polish space are equivalent:

A is analytic.
A is empty or a continuous image of the Baire space ω^ω.
A is a Suslin space, in other words A is the image of a Polish space under a continuous mapping.
A is the continuous image of a Borel set in a Polish space.
A is a Suslin set, the image of the Suslin operation.
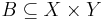There is a Polish space $Y$ and a Borel set $B\subseteq X\times Y$ such that $A$ is the projection of $B$ ; that is,

$A=\{x\in X|(\exists y\in Y)\langle x,y \rangle\in B\}.$

A is the projection of a closed set in X times the Baire space.
A is the projection of a G_δ set in X times the Cantor space.

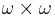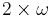An alternative characterization, in the specific, important, case that $X$ is Baire space, is that the analytic sets are precisely the projections of trees on $\omega\times\omega$ . Similarly, the analytic subsets of Cantor space are precisely the projections of trees on $2\times\omega$ .

Properties

Analytic subsets of Polish spaces are closed under countable unions and intersections, continuous images, and inverse images. The complement of an analytic set need not be analytic. Suslin proved that if the complement of an analytic set is analytic then the set is Borel. (Conversely any Borel set is analytic and Borel sets are closed under complements.) Luzin proved more generally that any two disjoint analytic sets are separated by a Borel set: in other words there is a Borel set containing one and disjoint from the other. This is sometimes called the "Luzin separability principle" (though it was implicit in the proof of Suslin's theorem).

Analytic sets are always Lebesgue measurable (indeed, universally measurable) and have the property of Baire and the perfect set property.

Projective hierarchy

Analytic sets are also called 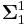$\boldsymbol{\Sigma}^1_1$ (see projective hierarchy). Note that the bold font in this symbol is not the Wikipedia convention, but rather is used distinctively from its lightface counterpart 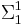$\Sigma^1_1$ (see analytical hierarchy). The complements of analytic sets are called coanalytic sets, and the set of coanalytic sets is denoted by 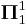$\boldsymbol{\Pi}^1_1$ . The intersection 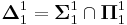$\boldsymbol{\Delta}^1_1=\boldsymbol{\Sigma}^1_1\cap \boldsymbol{\Pi}^1_1$ is the set of Borel sets.

References

El'kin, A.G. (2001), "Analytic set", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=A/a012410
Efimov, B.A. (2001), "Luzin separability principles", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=l/l061080
Kechris, A. S. (1995), Classical Descriptive Set Theory, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94374-9
Luzin, N.N. (1917), "Sur la classification de M. Baire", C.R. Acad. Sci. Paris Sér. I Math. 164: 91–94
N.N. Lusin, "Leçons sur les ensembles analytiques et leurs applications" , Gauthier-Villars (1930)
Moschovakis, Yiannis N. (1980), Descriptive Set Theory, North Holland, ISBN 0-444-70199-0
Martin, Donald A.: Measurable cardinals and analytic games. "Fundamenta Mathematicae" 66 (1969/1970), p. 287-291.
Souslin, M. (1917), "Sur une définition des ensembles mesurables B sans nombres transfinis", Comptes Rendus Acad. Sci. Paris 164: 88–91

Analytic set

Contents

Definition

Properties

Projective hierarchy

References